Math and Me
I was only required to take one semester of math to fulfill my math requirement as I was a freshman in college. I spent that semester taking calculus I and was thrilled to finish and presumably never need to take another math course. Over the years, I found that I did occasionally need some household math – volume measurements, areas and the like . Meanwhile, I will share that I remain in awe of people who can look at a mathematical formula and instantly see the underlying relationships and the meaning packed into it.

Taking all this into account, therefore, it is strange that I have had a fascination with Fibonacci Numbers. Until recently, I could not remember where I first heard about them. However, in doing research for this blog I came across reference to a book The (Fabulous) Fibonacci Numbers by A. Posmentier and I. Lehman. Years ago I had been friendly with Posmentier’s wife and had seen the book in their apartment where I riffled through it. But, regardless of its hold on me, it turns out Fibonacci Numbers have enormous resonance within the natural world.
What is a Fibonacci?

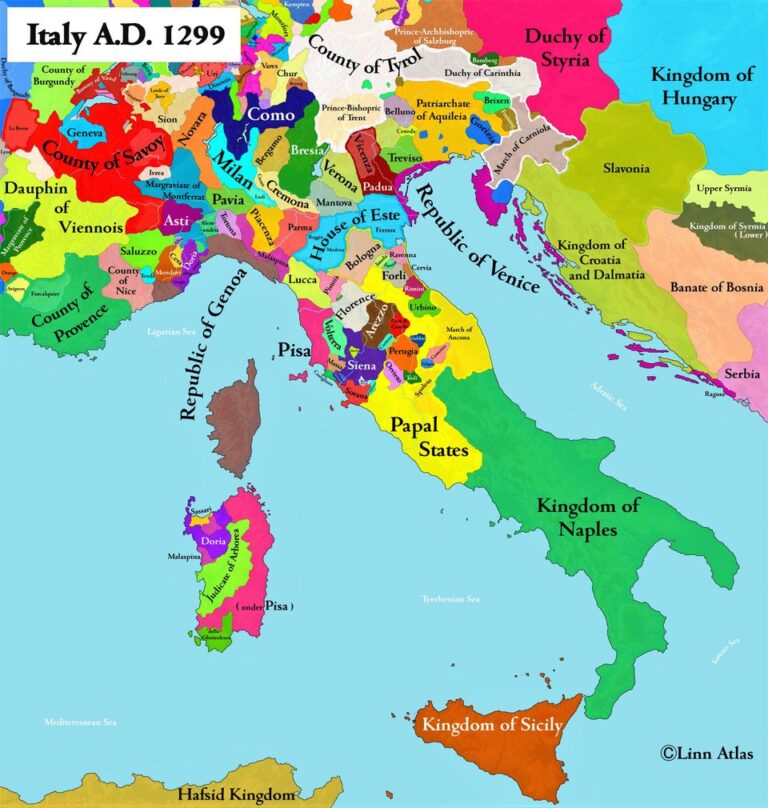
Actually, Fibonacci is a name. In fact, it is the name of an Italian mathematician (c. 1170- c.1240-1250), born in the Republic of Pisa, who popularized the Hindu-Arabic numeral system in the West. He was known variously as Leonardo Bonacci, Leonardo Pisano (Leonardo of Pisa) or Leonardo Bigollo Pisano (Leonardo the Traveler from Pisa). There is little biographical information about Leonardo so there is speculation that Fibonacci may be derived from fillius Bonaccii (son of Bonacci) although his father’s personal name was Guglielmo. During period family names did not exist so it is possible that Bonacci might be an extended family group. In any case, the name Fibonacci was only introduced in 1838 by the historian Guillaume Libri.
Actually there are no likenesses of Leonardo. The statue was erected simply as a tribute to the man and his work.
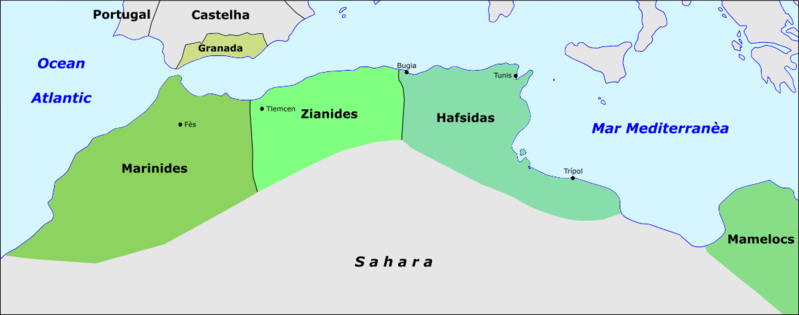
Leonardo’s father held a post as the commercial representative for the Republic of Pisa in the North African town of Bugia (in the province of Cabilia) on the Mediterranean, presently located in Algeria. It is believed that it was in Bugia that Leonardo was introduced to the Hindu-Arabic numeral tradition while accompanying his father. Although Leonardo wrote several books on mathematics, it was his Liber Abaci (Book of the Abacus / Book of Calculations), finished in 1202, which demonstrated an easier way to calculate numbers using Hindu-Arabic notation rather than the clumsier Roman Numeral system. Otherwise the book was devoted to how-to’s for business calculations.
The Fibonacci Sequence
Children initially learn to count, by ones. Then, with increasing boldness they learned to count by twos – both odd and even sequences. There are many other number sequences that fascinate mathematicians such as prime numbers . These consist of numbers that can be divided by two positive numbers only -themselves and one. This series goes 2, 3, 5, 7, 11, 13, 17…
The Fibonacci Sequence, with all due modesty, was already known in ancient India. However, it shows up in the Liber Abaci as a mathematical problem where the example discusses the rapid procreation of rabbits. This (Fibonacci) sequence runs 0, 1, 1, 2, 3, 5, 8, 13, 21…. where each new number is the sum of the two preceding numbers. These matters are exciting to mathematicians, so much so that there is even a journal devoted to it – The Fibonacci Quarterly However, except for an unusual affinity for the name, should we care?
Phyllotaxis
Just as people have recognizable features, so plants have stable features by which we know them. These characteristics include trunk type, bark texture and leaf shape. One of the other distinctive features is the relationship of the leaves to each other. Phyllotaxis or phyllotaxy describes the arrangement of the leaves on a plant stem. The word is from the ancient Greek with phyllon meaning “leaf” and taxis meaning “arrangement.” The concept of phyllotaxis was introduced by the naturalist Charles Bonnet from Geneva, Switzerland (1720-1793) in 1754.
There are three basic patterns for leaf placement on both herbaceous plants and trees. The first type is opposite where the leaves arise across from each other at the same node on the stem, basically appearing as pairs. The second is alternate – also referred to as spiral – where the leaves arise at different points along the stem at different nodes, appearing individually. This type of growth maximizes light exposure since the higher leaves do not overlap immediately lower ones. Finally, there is the whorled pattern where several leaves – minimally three – appear to grow out of the same point either on the stem or at the tip of the plant. As with everything else in the plant world, there are multiple variations on these themes.
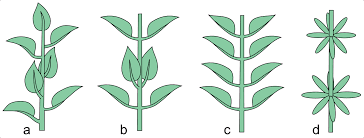



With all of the above as an introduction, we shall explore the relevance of Fibonacci numbers to Nature in the next installment.
If you are enjoying my work, perhaps you would be interested in my book, A Habit of Seeing: Journeys in Natural Science.

A very nice introduction to this world of numbers. Now I know what the sequence means. Nature, math, geometry all one. Thank you for the research. Looking forward to part II.
I have read this article three times now, and I finally feel that I understand the connection.. As alwa ys, you describe the histor y beatifully.
Keep up the good work. I’m looking forward to part two.
This was a very fascinating topic! I knew math can be found throughout the universe and especially in nature, but hadn’t really visualized ‘how’ until reading this post. Thank you for sharing your knowledge!