How Many Petals Does it Take to Make a Beautiful Flower?
I could only find one plant with a single petal. That plant is a native of southeast Asia and a member of the Fabaceae family, Afzelia xylocarpa.
Although calla lilies (Zantedeschia aethiopica – Family Araceae) are frequently mentioned as having one petal, the white petal-like structure overarching the rest of the fruiting body is actually a spathe which is a type of modified leaf.


Some plants have 2-petal flowers. These include the weedy Asiatic dayflower, Commelina communis, Family Commelinaceae.
Another common weed with a two-petalled flower is Circaea canadensis, Family Onagraceae. Both of these plants can be seen growing along Riverdale streets during late summer. It is Circaea that produces those little barbed fruits that get stuck all over your clothing.


Moving along to check some of the other Fibonacci numbers, there are plants with three-petalled flowers: lilies, trillium and irises.


Although careful examination of iris flowers would lead you to believe that the plant actually has six-petalled flowers. However, three of the assumed petals are, in fact, elaborate sepals. Sepals are the outer green part of a flower that enclose the developing bud but they can surprise us by frequently imitating petals.
Just to extend this further, roses and buttercups have 5 petals, delphiniums have 8, marigolds have 13, Black-Eyed Susans have 21. Many other plants share these Fibonacci numbers.
However, it would be unfair of me not to mention that there are also flowers with non-Fibonacci petal numbers.
Four petal flowers include hydrangeas, bleeding hearts and evening primroses. And six petal flowers include mayapples (Podophyllum peltatum), Solomon’s Seal ( Maianthemum stellatum)and yucca (Yucca filamentosa).



Odds & Ends
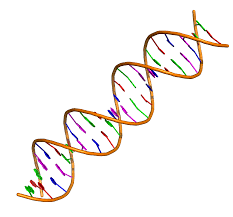
A few bits of interesting trivia: I bought a course from The Great Courses entitled The Shape of Nature. I expected it to be a botany course but, instead, it turned out to be about the mathematics of knots. I was a bit surprised since I could not even imagine a mathematical interest in knots. While most of the material was not easily graspable for me , it did mention that DNA helices are examples of knots in nature. It turns out that the helix is 34 angstroms long by 21 angstroms wide for each full cycle of the double helix spiral.
By now, I – and you -realize that these too are Fibonacci numbers!
Interest in the Fibonacci Sequence is not limited to nature studies. David MacDonald has composed an performed a lovely piece of music based on it.
It is tempting to wonder whether there is a specific lesson or meaning that could be derived from all this information. At present, I am content to simply contemplate this material with wonder. If anyone would like to make suggestions, I would be interested in their thoughts.
If you have enjoyed these pieces, you may enjoy my book A Habit of Seeing: Journeys in Natural Science

It is a world full of wonders. Thank you for sharing some of them. Enjoy
Thank you for sharing your research of the wonders of nature. Amazing!
Hello SJ –
Thanks for the plethora of pictures to accompany your latest blog.
Think about attending the VCPk Alliance Lawn Party on 6/24. https://vancortlandt.org/lawnparty/
Thank you. So interesting!
Esther Lewittes